수십억 개의 파라미터를 자랑하는 GPT-4도 4×4 자릿수 곱셈에서는 95%가 넘는 실패율을 보입니다. 하버드와 MIT 연구진이 모델을 역설계하여 밝혀낸 바에 따르면, 문제는 트랜스포머가 곱셈에 필요한 장거리 의존성(long-range dependency)을 학습하지 못한다는 것입니다.

핵심 포인트:
- 표준 미세조정의 치명적 결함: 4×4 곱셈에서 정확도 1% 미만. 12층 모델로 확장해도 동일한 결과. 경사하강법이 초기/말단 자릿수만 학습하고 중간 자릿수에서 로컬 최적값에 갇힘
- 암묵적 사고연쇄(ICoT)의 비밀: 100% 정확도 달성. 어텐션을 이진 트리 구조로 조직화해 부분곱을 “캐싱”하고 “검색”하는 메커니즘 구현
- 실용적 해결책 제시: ICoT 없이도 보조 손실(auxiliary loss)만 추가하면 99% 정확도 달성 가능. 실무 적용 가능성 입증
간단해 보이는 산술, 거대 AI는 왜 실패할까
GPT-4는 복잡한 코드를 작성하고 법률 문서를 분석하지만, 단순한 곱셈에서는 놀랄 만큼 취약합니다. 실험 결과 2개 숫자 곱셈에서는 95% 정확도를 보이지만, 3개 숫자는 30%, 4개 숫자는 5%로 급격히 떨어지고 그 이상은 거의 0%에 가까웠습니다.
왜 이런 일이 벌어질까요? 연구진은 4×4 곱셈을 성공하는 모델(ICoT)과 실패하는 모델(표준 미세조정)을 역설계해 그 차이를 밝혀냈습니다.
곱셈이 어려운 진짜 이유: 장거리 의존성
곱셈은 단순해 보이지만 복잡한 장거리 의존성을 요구합니다. 예를 들어 네 자릿수 숫자 두 개를 곱할 때 k번째 자릿수를 계산하려면, 인덱스 합이 k 이하인 모든 부분곱(aᵢ×bⱼ)을 고려해야 합니다.
더 중요한 건 이전 자릿수에서 넘어온 올림수까지 추적해야 한다는 점입니다. 결국 각 자릿수 계산은 멀리 떨어진 여러 입력 숫자들의 복잡한 상호작용에 의존합니다.

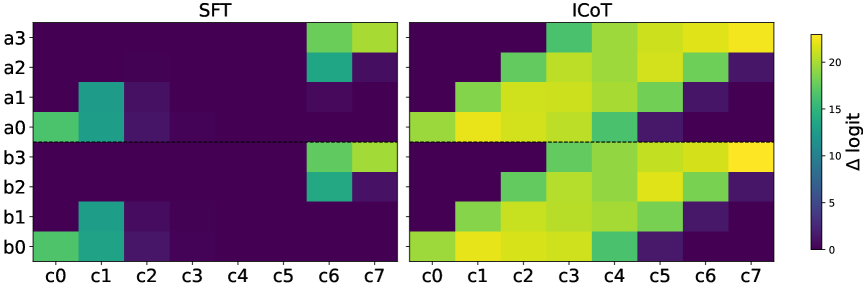
로짓 어트리뷰션(logit attribution) 분석 결과, 표준 미세조정 모델은 이런 의존성을 전혀 학습하지 못했습니다. 반면 ICoT 모델은 필요한 모든 부분곱의 정보를 정확히 인코딩했습니다.
성공 사례의 비밀: 어텐션 트리와 기하학적 구조
ICoT 모델은 어떻게 성공했을까요? 연구진이 발견한 메커니즘은 놀라울 정도로 정교했습니다.
첫 번째 층: 각 타임스텝에서 어텐션 헤드가 정확히 한 쌍의 숫자(aᵢ, bⱼ)에만 집중합니다. 이를 통해 부분곱을 계산하고 그 결과를 해당 타임스텝의 히든 스테이트에 “캐싱”합니다.
두 번째 층: 나중 타임스텝에서 솔루션 토큰을 예측할 때, 어텐션이 필요한 부분곱이 저장된 이전 타임스텝들을 선택적으로 “검색”합니다.
이는 마치 이진 트리를 시간 축에 걸쳐 펼쳐놓은 것과 같은 구조입니다. 각 노드는 특정 부분곱을 담당하고, 상위 노드는 하위 노드의 결과를 조합합니다.
더 흥미로운 건 기하학적 표현입니다. 모델은 숫자를 푸리에 기저(Fourier basis)로 인코딩하고, 어텐션 헤드 출력은 민코프스키 합(Minkowski sum)으로 부분곱을 구현합니다. 3D PCA 시각화 결과, 0부터 9까지의 숫자들이 오각기둥(pentagonal prism) 구조를 형성했습니다. 짝수와 홀수가 각각 오각형을 이루며 평행하게 배치되는 이 구조는 효율적이고 직관적인 표현 방식입니다.

표준 학습은 왜 실패하는가
표준 미세조정 모델의 학습 과정을 자세히 들여다보면 문제가 명확히 드러납니다. 토큰별 경사도(gradient)와 손실(loss)을 추적한 결과, 모델은 처음 두 자릿수(c₀, c₁)와 마지막 자릿수(c₇)만 빠르게 학습했습니다. 이후 c₂도 학습했지만, 중간 자릿수(c₃~c₆)는 끝까지 학습하지 못했습니다.
중간 자릿수만 경사도를 받고 있음에도 손실이 정체된다는 건, 모델이 로컬 최적값에 갇혔다는 의미입니다. 장거리 의존성을 포착하지 못한 채 더 이상 개선되지 않는 것입니다.
흥미롭게도 모델을 12층 8헤드로 키워도 결과는 동일했습니다. 규모 확장만으로는 해결되지 않는 구조적 문제였습니다.
ICoT 없이도 해결할 수 있다
연구진은 한 가지 간단한 해결책을 제시했습니다. “running sum”을 예측하도록 하는 보조 손실을 추가하는 것입니다.
곱셈에서 각 자릿수를 계산하려면 중간값 ĉₖ(부분곱의 합과 이전 올림수의 합)가 필요합니다. 이 중간값을 선형 회귀 프로브로 예측하도록 보조 손실을 추가하면, 모델에게 적절한 귀납적 편향(inductive bias)을 제공하는 셈이 됩니다.
결과는 놀라웠습니다. ICoT 없이도 2층 모델이 99% 정확도를 달성했습니다. 학습 과정도 달라졌습니다. 초기/말단 자릿수부터 시작해 안쪽으로 순차적으로 학습하며, 모든 자릿수의 손실이 0으로 수렴했습니다.
물론 이 방법은 작업 특화적입니다. 하지만 핵심은 올바른 귀납적 편향이 장거리 의존성 학습 문제를 해결할 수 있다는 것입니다.
LLM 설계에 던지는 메시지
이 연구가 던지는 메시지는 명확합니다. 현재 언어모델의 표준 학습 방식—트랜스포머에 경사하강법과 자기회귀 손실을 적용하는 것—만으로는 장거리 의존성을 학습하기 어렵습니다.
GPT-4가 복잡한 추론을 수행하면서도 단순한 곱셈에 실패하는 이유가 바로 여기 있습니다. 중간 단계에 대한 명시적 감독이나 적절한 아키텍처 개선 없이는 모델이 필요한 구조를 학습하지 못합니다.
실무적으로는 중간 추론 단계에 대한 감독(process supervision)이 중요합니다. ICoT처럼 명시적 사고연쇄를 점진적으로 내재화시키거나, 보조 손실로 중간 결과를 예측하게 하는 방식이 효과적입니다. 이는 수학 문제뿐 아니라 복잡한 추론을 요구하는 다양한 작업에 적용 가능한 원칙입니다.
참고자료:
답글 남기기